• 调研近年因果发现的最新研究
• 将”因果发现”与”根因分析”以及”基于因果图的因果发现”等概念理清关系
• 从优化的角度重新看待三类因果发现算法, 这可以帮助我们借鉴已有方法到自己的工作中。
• 总结用于因果发现的各种包, 以及Github上star较多的Repositories

1. 因果三阶梯

Causal discovery(CD) 包含三个层次 [1]:

• 关联 Association: A、B相关
• 干预 Intervention: 改变A的时候, B如何改变
• 反事实 Counterfactuals: 要想改变B, 应该如何改变A

事实上, 许多CD的方法都仅能做到前两个阶段。”反事实”通常是不可实现的, 因为”反事实”要求在与历史完全相同的环境因素下探究决策对个体的影响。

2. 因果的本质、数学表达 与 因果结构学习

这一节的分析源自下面对三类causal structure learning方法挖掘的因果本质的思考。后文中已经分析得出，三类causal structure learning方法发现的因果都只停留在由“条件依赖”或者“回归”所刻画的“关联关系”，而非真正的因果关系，因此本节的主题是

• 调研casual discovery和causal structure learning之间的区别（这个问题和哲学上的因果定义有关）
• 除了DAG表示的因果图外，还有哪些表征因果的模型范式（DAG因果图就是节点代表变量，边代表直接原因的图模型）

要分析causal discovery和causal structure learning之间的区别，有以下思路：

• 已知causal structure learning中，已经用不同的模型对因果进行了定义，这种定义或是定性的、或是定量的，因此这类方法本质上就是在根据每种方法的定义，从数据中拟合所谓的“因果”。因此causal structure learning可以视为“学习以模型定义的因果”的一类方法

• 那除了用模型定义的因果，还有哪些定义呢。

2.1 因果的本质

文献[14]从哲学、社会学等层面探究了因果在AI领域的定义，在Section 6.5中提到了一个关键问题：“因果是确定性的还是概率性的？”，以下是一些结论：自古以来，因果这个概念都不具备一个统一的定义。自古以来，因果总是与决定论、物理必然性和逻辑必然性联系在一起（即：确定性）。但在现代科学所研究的因果理论几乎都是概率性的，即以概率论和统计学论为基础的。但也有部分确定性的表述，这种表述大多源自于工程学，是一种不证自明方法（这里我理解，在工程学里总有“改变A，基于设计原理，B就一定会改变，并且B只受A控制，因此AB是因果关系”的表述，这种工程学上的因果显然是确定性的）。

其实，因果在统计学上的定义也并未统一，文献[16]中列出了三种主要的观点，下文说明一种较常见的观点，来自于Good[17]：

事件 $F$ 是事件 $E$ 的原因需要满足：

1. 事件 $E$ 和 $F$ 同时成立（对有时间约束的事件则是$F_t \leq E_t$）

2. $P(E|H)<1, P(F|H)<1$ ，其中$H$包含两部分：

   • $H1$ : 所有的自然法则

   • $H2$ : 所有被认为是理所当然的真实背景条件

3. $P(E|FH) > P(E|\bar{F}H)$

Good在后续的研究[18][19]中试图给出因果关系的一种定量描述。$F$ 对$E$ 的潜在因果趋势可以由下式度量

$$ \log \frac{P(\bar{E}|\bar{F}H)}{P(\bar{E}|FH)} $$

where $H$ consists of all laws of nature and the background conditions before $F$ started. Thus for $F$ to be a potential cause of $E$, the two must be probabilistically dependent conditional on $H$. The (actual causal) degree to which $F$ caused $E$ is the limit, as the sizes of the events tend uniformly to zero, of the strength of the network of causal connections between $E$ and $F$. Here the strength of a link from $F$ to $E$ is measured by the tendency of $F$ to cause $E$; the strength of the network as a whole is a function of these link strengths which takes into account interactions amongst causes.

根据以上思路，可以分析得到：

• 因果在哲学上的定义一般都是确定性的，但在现代科学中，通常被定义为概率性的。之所以被如此定义，一方面是有部分前人的工作也如此定义；另一方面，经典的概率足以模拟人类推理的几乎所有方面[15]。从这个角度上来讲，概率性因果是对确定性因果的一个更广义的描述。
• 站在概率性因果的角度，因果发现可以被称之为，在数据中发现概率结构的工作（即因素A的概率分布变化时，因素B的概率分布是否变化），其本质都是在拟合一个概率模型。从这个角度来说，概率模型也可以用于因果发现。

2.2 因果结构学习

近三十年来, 因果学习的工作一般聚焦于”因果结构学习(casual structure learning)”, 所得到的结构因果模型(structural causal model, SCM) 对因果进行了概率、统计上的定义，并用恰当的模型来描述因果结构。SCM包含两个部分:

• Graphical models: 由图模型表示的因果关系, 其中节点表示随机变量, 有向边表示因果方向
• Structural equations: 在图模型中, 有向边上的因果效应, 由函数式表示

graphical model则是structure causal model的一种，也是受广泛研究的一种。

[1]中对SCM有以下论述

“structural causal models” (SCM), which consists of three parts: graphical models, structural equations, and counterfactual and interventional logic.

Graphical models serve as a language for representing what agents know about the world. Counterfactuals help them articulate what they wish to know. And structural equations serve to tie the two together in a solid semantics.

[3]中则着重推崇了图模型作为因果模型的表达形式

Methods for extracting causal conclusions from observational studies are on the middle rung of Pearl’s Ladder of Causation, and they can be expressed in a mathematical language that extends classical statistics and emphasizes graphical models.

Various options exist for causal models: causal diagrams, structural equations, logical statements, and so forth. I am strongly sold on causal diagrams for nearly all applications, primarily due to their transparency but also due to the explicit answers they provide to many of the questions we wish to ask.

……

Pearl defines a causal model to be a directed acyclic graph that can be paired with data to produce quantitative causal estimates. The graph embodies the structural relationships that a researcher assumes are driving empirical results. The structure of the graphical model, including the identification of vertices as mediators, confounders, or colliders, can guide experimental design through the identification of minimal sets of control variables. Modern expositions on graphical cause and effect models are Pearl (2009) and Spirtes et al. (2000).

综上所述，casual discovery / probabilistic model / structure casual model / casual graph 之间的关系为

**Remark**: (1) 格兰杰因果应该属于structure casual model，但不一定属于图模型；(2) 图模型不仅包括DAG，还有其他类型的图。

2.3 因果与统计模型的关联与区别

上文中提到，广义上讲，因果学习的本质是学习一个概率模型（概率模型可以被视为统计模型）。但概率模型 （或统计模型）与 因果 是两个完全不同的概念。

首先，明确一个关系，即：根据因果三阶梯，从上到下分别为“关联”“干预”“反事实”，其中关联是上述两个概念的基础，而干预和反事实才是因果特有的层次。[20]对关联和因果给出了明确的分界线。

• 关联：可以用分布函数来定义，例子：相关性、回归、依赖性、条件独立性等
• 因果：不能只用分布函数来定义，例子：影响、混淆、干扰等。因果不能从关联中推导出，甚至不可以只从统计关联的角度上定义。

从数学的角度上，任何因果分析的数学方法都必须获得新的符号来表示因果关系。概率符号对于表示因果关系来说是不够的。

• 举例来说，概率相关的数学语言不允许我们表达“症状不导致疾病”这一简单事实，更不允许我们从这些事实中得出数学结论。我们只能说，两个事件是相互依赖的——这意味着，如果我们找到一个，我们就可以预期遇到另一个，但我们无法区分统计依赖性（由条件概率 P 量化的疾病症状）和因果依赖性，我们在标准概率演算中没有对此关系的表达式[20]。

这是我们为因果关系建立一套新的数学表达的动机。

2.4 因果分析中的数学表示

Structural Causal Models

• Structure Equations：变量-下标形式 / 带 $do$ 操作符的形式：

  $$ 𝑃(𝑌_𝑥 = 𝑦)⟺𝑃(𝑌=𝑦|𝑠𝑒𝑡(𝑋=𝑥))⟺𝑃(𝑌=𝑦|𝑑𝑜(𝑋=𝑥)) $$

  • $P(Y_x = y)$：$Y$ 是一个随机变量，当随机变量 $X=x$ 时 $Y$ 在总体中达到 $y$ 值的概率。

  • $P(Y=y|do(X=x))$：当 $X=x$ 均匀的施加在每一个个体上时，$Y=y$ 发生的概率，常用于控制实验。

• Graphical Models：因果假设编码在缺失的链接中——两个变量之间有连接只代表存在因果关系的可能性，而没有连接则代表没有因果。可以辅以方程式来表达因果之间的定量关系。

表达因果效应大小

• $Cov(X, Y)$：给定由以上模型表征的因果假设后，可以用协方差表示因果效应的大小，辅助从观察到的非实验数据中估计因果参数。

干预——数学表达

干预的基础是结构方程（SEM），并通过$do$运算符完成。

• $do(x)$：模拟了一种物理世界的交互——在给定的SEM中，删除原模型中X变量的函数，并人为替换变量为一个常数 $X=x$。如下图所示
  • $P(z, y | do(x))$：变量 $Y$ 和 $Z$ 的干预后分布，即表示对所有个体均实施了$X=x$ 后，变量 $Y$ 和 $Z$ 的联合分布
  • $P(z, y, x)$：变量的干预前分布
• 记干预前的因果模型为$M$，干预 $X=x$ 后的因果模型为$M_x$
  • $P_M (y|do(x)) ≜ P_{M_x}(y)$：在干预前的模型 $M$ 中实施干预 $do(x)$ 后 $Y$ 的分布，等价于在干预后模型 $M_x$ 中$ Y$ 的分布。

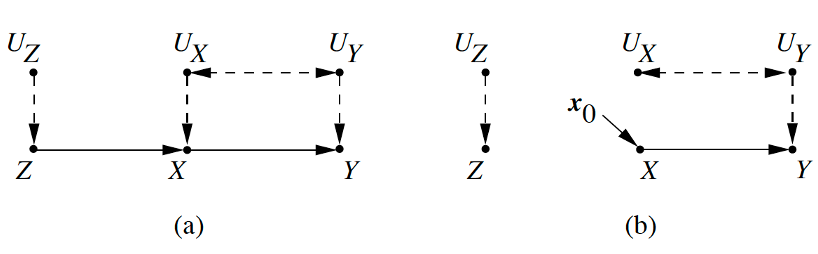
干预的效果表示

• Causal effect：$P(Y=y|do(x))= \sum_z P(z, y|do(x))$
• Measurements
  • Average Difference：$E(Y|do(x_0^{‘})) -E(Y|do(x_0))$
  • Experimental Risk Ratio：$\frac{E(Y|do(x_0^′))}{E(Y|do(x_0))}$

反事实——数学表达

• $Y_x (u)$：在变量曾被设置（has been set）为 $X=x$ 的情况下，个体 $u$ 得到的 $Y$ 变量的值
• $Y_x (u)≜Y_{M_x} (u)$：Unit-level的反事实，定义为在干预后模型 $M_x$ 中，个体 $u$ 得到的 $Y$ 变量的值。
  • 反事实可以被视为特定情境因素（与过去某个时间的所有因素一致）下的干预。
  • 反事实一般研究特定情境因素下，个体的干预结果。干预则一般研究决策的平均影响情况

2.5 反事实推理

从上文可以看出，因果区别与一般的统计模型，其中干预和反事实起到了决定性的作用。本节将先区别干预与反事实的区别，然后阐述反事实推理的基本步骤。

从目标的角度

• 干预：回答“如果现在干预变量X，那么对Z会发生什么变化？”
• 反事实：回答“如果在过去某个时间干预变量X，Z会发生什么变化？”

其区别在于

• “干预”改变但不与观察到的世界相矛盾，因为干预前后的世界处于不同的时间

• “反事实”则与已知事实相冲突

注：二者并不是被严格区分的，也有研究不区分二者，这是一种哲学/文化上的差别

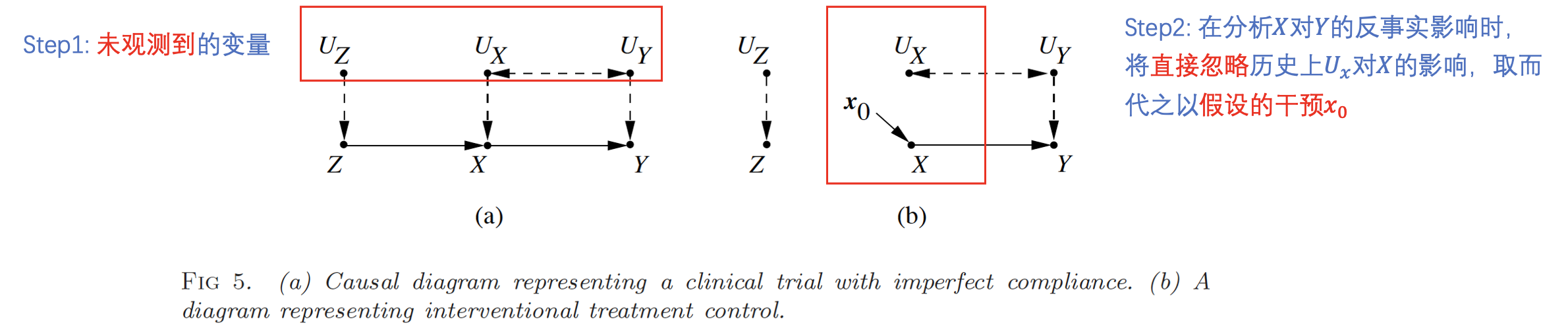
反事实推理的基本步骤

Background：SCM及其当中的参数

1. Step1: 外展——为每个观测变量设置一个在过去可能未观测到的变量集合$U$，基于历史观测学习集合$U$

2. Step2: 干预——为反事实推理建立新的干预模型，其中干预操作将会代替SCM中的一个（或多个）变量

3. Step3: 预测——将历史未观测变量$U$以及干预操作代入修改后的SCM，进行反事实推理

反事实（Counterfactual）推理——以确定性模型为例

对于概率型模型，则需要针对变量的所有情况进行考虑。其中“预测”则由“求概率”转为“求期望”。

下面的指标可以用于评估某个操作是否对未来有影响[20]，此外还有多种指标，如

$$ P N(x, y)=P\left(Y_{x^{\prime}}=y^{\prime} \mid X=x, Y=y\right) \\ E T T=P\left(Y_x=y \mid X=x^{\prime}\right) $$

2.6 支撑材料

“结构学习本质上是一个模型选择问题，选择一个给定数据集上最能够描述数据依赖的模型。因果结构学习是结构学习中的一种特例，其学习了一个因果图”。这个观点是被普遍接受的。

Remark：结构学习的三种方法（基于约束、基于分数、基于函数）本质上都可以细分为通过组合/搜索算法，来识别因果结构 [13]

Structure learning is a model selection problem in which one estimates or learns a graph that best describes the dependence structure in a given data set (Drton & Maathuis 2017). Causal structure learning is the special case in which one tries to learn the causal graph or certain aspects of it, and this is what we focus on in this article.

—— Heinze-Deml, C., Maathuis, M. H., & Meinshausen, N. (2018). Causal structure learning. Annual Review of Statistics and Its Application, 5, 371-391.

Q1：除DAG外，还有哪些因果图

摘自 [13]

Other types of graph used to represent causal structure include Partially Oriented Induced Path Graphs (POIPGs)[190, 228], SingleWorld Intervention Graphs (SWIGs) [24, 201, 202], σ-connection graphs [56], undirected graphs[11], interaction and component graphs for dynamic systems [40], Maximal Almost Ancestral Graphs (MAAGs)[231], psi-ECs [110], Patterns [274], and arid, bow-free, and ancestral ADMGs [19].

There are also other types of assumptions relating to the functional form of the structural relationships (e.g., linear or non-linear) as well as the parametric form of the marginals and the errors (e.g., Gaussian or non-Gaussian).

Q2：大数据对因果发现的贡献

由三阶梯定义的因果通常是难以推断的，因为大多数情况下，实验人员都难以“干预”，更别说“反事实”。此外，可能存在“未被观测的潜在因素”、“因果知识通常是非先验的（我理解是，非先验导致难以反事实）”也是阻碍因果发现与估计的因素之一 [13]。

Unfortunately, in many cases, it may not be possible to undertake such experiments due to prohibitive cost, ethical concerns, or impracticality. For example, to understand the impact of smoking, it would be necessary to force diferent individuals to smoke or not-smoke. Researchers are therefore often left with non-experimental, observational data. In the absence of intervention and manipulation, observational data leave researchers facing a number of challenges: Firstly, observational datasets may not contain all relevant variables - there may exist unobserved/hidden/latent factors (this is sometimes referred to as the third variable problem). Secondly, observational data may exhibit selection bias - for example, younger patients may in general prefer to opt for surgery, whereas older patients may prefer medication. Thirdly, the causal relationships underlying these data may not be known a priori - for example, are genetic factors independent causes of a particular outcome, or do they mediate or moderate an outcome? These three challenges afect the discovery and estimation of causal relationships

因此，大数据、或机器学习算法在因果发现问题中扮演的角色可以描述为

• 大数据的数据量级弥补了观察不充分导致的“未观察、漏观察”、“选择偏差”，即大数据使得我们可以观察到更多的变量，当观察足够充分时，推断出真实因果的概率就越大。
• 大数据也可以以数据量级减轻选择偏差（我理解是：虽然年轻人可能更倾向于选择整形手术，但随着样本增多，也可以找到倾向于做整形手术的老年人）。
• 大数据可能可以帮助我们进行反事实，例如对于一个周期系统，通过足够多周期的观察，我们也许可以找到一个时间点，只有一个原因变量发生变化，而其他所有变量都与历史保持一致，这种场景有利于推断因果反事实。

此外，对比实验数据（即存在“干预-效果”结构的数据）以及观测数据（即只包含非主动干预以及被动观测的数据），观测数据可以提供更好的统计能力和可推广性 [13]。

3. Casual Structure Learning

3.1 Casual structure learning的三类方法

Casual structure learning的经典分类方法可分为三个主要类别：constrain-based, score-based, functional casual model [2]，还有一些hybird method，此处不列出。

Remark：也有文章[13]提出“constraint-based, score-based, those exploiting structural asymmetries, and those exploiting various forms of intervention”的分类方法，这种分类方法比较新，可能对近期（2022）工作有较好的适应性。

• Constraint-based methods: 这类方法依赖随机变量间的条件独立性测试(conditional independency test) 探究变量间的因果结构

  • 在传统的PC算法中, 为了简便的推导出因果结果, 基于CI定义了两种图上的结构, 即 V-structure / D-separation, 这两种结构可以辅助推导出因果的结构与方向。具体的, PC首先构造一个完全图, 然后通过两两变量间的independency test删除某些无向边, 然后基于CI test以及V-structure / D-separation, 确定其余边的方向或删除某些边。

  • 缺点:

    1. 不能存在未观测的混杂变量, 该条件在大数据的情况下很难满足, 但存在如FCI的算法放宽了该限制
    2. 根据因果信念假设, 只能根据条件独立性来判断因果关系, 因此需要非常多且高质量的数据, 如果数据较少, 则条件独立性假设测试可能会互斥
    3. 对于分叉结构以及对撞结构, 该类算法无法根据条件独立性分辨马尔可夫等价类(Markov equivalent class), 因此对局部因果关系的判别不足
    • Markov equivalent class: 拥有相同d分离结构的因果图并且具有相同条件独立性关系的因果图被称作马尔可夫等价类, 无法根据条件独立性分辨因果方向。

• Score-based methods: 这类方法首先指定因果父节点到子节点之间的函数关系, 然后以某个分数, 如AIC / BIC, 为优化目标, 优化得到图结构以及相关参数。

  • 如NOTEARS假设函数关系为 $x=\sum w_x f(P_a(x))$ , 其中 $w_x$ 是变量 $x$ 的权重, $P_a(x)$ 是其因果父节点
  • 缺点:
    1. 该方法也会得到马尔可夫等价类。
    2. 由于要找到最优分数, 就要搜索全部的图, 这是一个NP-hard的问题, 复杂度极高且容易陷入局部最优。

• Functional casual model: 这类方法往往探究两个已有关联的变量之间的因果方向。首先对数据与因果函数做出假设, 然后通过测试两个变量之间是否满足关联函数, 来判断二者之间的关联方向。

  • 如LiNGAM假设因果之间满足线性关系, 且数据中的噪音为高斯噪声

  • 该类方法由于进行了严格的假设, 且一般会根据函数的拟合程度来找到唯一的因果方向, 因此一般不会出现马尔可夫等价类

  • 注意, FCM一般是探究两个变量之间因果关系的方法, 如[4]所述。该类方法的缺点是对数据特性以及因果有较强的假设。

    Determining causal relationships between two variables is a fundamental and challenging causal discovery task (Janzing et al., 2012). Conventional constraint-based and score-based causal discovery methods identify causal structures only up to Markov equivalent classes (Spirtes et al., 2001), in which some causal relationships are undetermined. To address this challenge, properly constrained functional causal models (FCMs) have been proposed. FCMs represent the effect as a function of its cause and independent noise and can help identify the causal direction between two variables by imposing substantial structural constraints on model classes, such as additive noise models (ANMs)

需要指出的是: 图模型只是一种因果关系的表示方式, 但该表示方式不是必要的。

上述三类方法, 由于其假设不同、检验方法不同, 因此挖掘出的”因果”具有不同含义(即因果图中的有向边具有不同的含义), 分属不同的因果阶梯:

• Constraint-based: 该类方法通过一系列变量之间的CI, 学习变量之间的因果关系。 该类方法挖掘出的因果本质是”条件依赖“, 这类依赖属于”关联“层面。
• Score-based / Functional causal model: 该类方法首先定义了因果变量之间满足的函数关系, 前者优化全局得分函数来确定变量间的因果, 后者采用穷举优化算法搜索变量间的因果。这两类方法挖掘出的因果本质是由”回归关系”表示的”关联”。

Q3：CD与RCA的关系

此外, 强调一下Root Cause Analysis(RCA)与CD的关系, 即: 一般的RCA更关注Causal discovery的前两个等级, 即探究”什么和异常相关？””什么导致了异常？”, 这就是为何许多RCA的方法都只考虑了关联、推理, 因此Causal discovery和RCA的关系如下:

3.2 从优化的角度分析三类方法

为了理解三类Casual structure learning的方法, 这里从优化的角度对三类方法进行阐述。

首先用$\mathcal{G}$表示$d$个节点所构成的有向图空间。对 $\forall G(\boldsymbol{M}) \in \mathcal{G}$ , 用 $\boldsymbol{M}$ 表示对应的邻接矩阵, 反过来, 用 $G(\boldsymbol{M})$ 表示以 $\boldsymbol{M}$ 为邻接矩阵的有向图。元素 $M_{i,j}=1$ 表示存在因果关系 $\boldsymbol{x}_i \rightarrow \boldsymbol{x}j$ ，$M{i,j}=0$ 表示不存在因果关系。 $\boldsymbol{X}=[\boldsymbol{x}_1, \cdots, \boldsymbol{x}_d] \in \mathbb{R}^{n \times d}$ 表示 $d$ 维的观测数据, 其中每个数据观测 $n$ 次。$\mathbb{D}$ 表示由 $d$ 个节点组成的有向无环图集合。

3.2.1 Constraint-based Method

基于约束的算法利用 从一系列统计测试中获得的一组条件独立性结果 来恢复因果图。

当从数据 $\boldsymbol{X}$ 中已经学习到每一对变量间条件独立检验的最小测试统计量，如p-value，因此可以构造出测试统计量矩阵 $\boldsymbol{P}$ ，其中对角线上的元素均为0，元素 $P_{i,j}$ 表示 $\boldsymbol{x}_i , \boldsymbol{x}_j$ 间的条件独立性检验的测试统计量，假设检验的显著性水平为 $\alpha$ 。 $f$ 表示条件独立检验统计量的函数， $Q$ 表示用于评价得到的统计量矩阵与图 $G$ 的拟合程度的函数。

该类方法的优化问题表述为:

$$ \begin{array}{} \min : & Q(\boldsymbol{M}, f(\boldsymbol{P}, \alpha)) \\ s.t. & G(\boldsymbol{M}) \in \mathbb{D} \\ var: & \boldsymbol{M} \in\{0,1\}^{d \times d} \\ \end{array} $$

**举例**: 如在PC[5]算法中，存在假设检验 $\left\{\begin{array}{} H_0: & \boldsymbol{x}_i \perp \boldsymbol{x}_j \\ H_1: & \boldsymbol{x}_i \perp / \boldsymbol{x}_j \end{array}\right.$ ，当测试统计量小于显著性水平时， $H_1$ 成立，即有

$$ Q(\boldsymbol{M}, f(\boldsymbol{P}, \alpha))=\sum_{i, j=1: \mathrm{d}} M_{i, j} \cdot\left(P_{i, j}-\alpha\right) $$

表示从数据中得到的(条件)独立约束在图得到的(条件)独立约束集合中未出现的数量。

3.2.2 Score-based Method

基于得分的算法最大化图 $G$ 与观测数据 $\boldsymbol{X}$ 之间的适应度, 来构建因果结构。该类方法的优化问题表述为:

$$ \begin{array}{ll}\max &S\left( \boldsymbol{M} ,\boldsymbol{X} \right) \\ \text{s.t.} &G\left( \boldsymbol{M} \right) \in \mathbb{D} \\ \text{var} &\boldsymbol{M} \in \left\{ 0,1\right\}^{d\times d} \end{array} $$

其中DAG约束在[6]中被重写为 $\text{tr} \left( {}e^{\boldsymbol{M} \circ \boldsymbol{M} }\right) -d=0$ , 这使得目标函数可以被连续优化。$S(\cdot)$为图与观测助局之间的适应度得分, 可用的得分函数包括BIC(GES[7])、Bde[8]、Bge[9]。不同的方法往往采用不同的搜索算法在图空间中与哦话上述目标函数, 如: 贪心搜索(greedy search)[8]、顺序查找(order search)[10]、坐标下降[5]。

举例: NOTEARS[11]]中的得分函数为

$$ \mathcal{S}(\boldsymbol{M}, \boldsymbol{X})=\frac{1}{2 n} \sum_{t=1}^n\left\|\boldsymbol{x}_{t,:}-\boldsymbol{f}\left(\boldsymbol{M}, \boldsymbol{x}_{t,:}\right)\right\|_F^2 $$

$\boldsymbol{x}_{t,:} \in \mathbb{R}^{1 \times d}$ 表示第 $t$ 个观测样本，$f$ 为生成模型

3.2.3 Functional Causal Model

基于FCM的算法假设变量间的因果关系满足函数 $\boldsymbol{x}_j=f(\boldsymbol{x}_i,\boldsymbol{e}j;\boldsymbol{\theta}{i,j})$ , 其中 $\boldsymbol{x}_i, \boldsymbol{x}_j$ 分别为直接原因变量、果变量， $\boldsymbol{e}_j \in \mathbb{R}^{n}$ 表示一些不可测量因素或噪音。 $\boldsymbol{\epsilon}=[\boldsymbol{e}_1, \cdots, \boldsymbol{e}_d]$ ， $\boldsymbol{\theta}$ 为模型参数。下式中用 $L(\cdot)$ 表示用于衡量参数 $\boldsymbol{\theta}$ 的模型的预测值与实际观测的数据 $\boldsymbol{x}_j$ 间的拟合程度的函数。该类方法的优化问题表述为:

$$ \begin{array}{} \min : & \sum_{i, j=1: \mathrm{d}} M_{i, j} \cdot\left(L\left(\boldsymbol{x}_j, f\left(\boldsymbol{x}_i, \theta_{i, j}\right)\right)+Q\left(\boldsymbol{x}_i, \boldsymbol{x}_j-f\left(\boldsymbol{x}_i, \theta_{i, j}\right)\right)\right) \\ s.t. & G(M) \in \mathbb{D} \\ var: & \boldsymbol{\theta}, \boldsymbol{M} \in\{0,1\}^{d \times d} \end{array} $$

设有假设 $H_1: \boldsymbol{x}_i \perp (\boldsymbol{x}_j - f(\boldsymbol{x}_i,\boldsymbol{\theta}_{i,j})$ ，$Q\left(\boldsymbol{x}_i, \boldsymbol{x}_j-f\left(\boldsymbol{x}_i, \theta_{i, j}\right)\right)$ 表示 $\boldsymbol{x}_i$ 和 $\boldsymbol{x}_j-f\left(\boldsymbol{x}_i, \theta_{i, j}\right)$ 之间的独立性检验的测试统计量，当其小于显著性水平 $\alpha$ 时接受 $H1$ （这种方法对应于一类假设检验方法：regression-based independence test）。

Reference

[1] Pearl, J. (2019). The seven tools of causal inference, with reflections on machine learning. Communications of the ACM, 62(3), 54-60.

[2] Glymour, Clark, Kun Zhang, and Peter Spirtes. “Review of causal discovery methods based on graphical models.” Frontiers in genetics 10 (2019): 524.

[3] Goldberg, L. R. (2019). The Book of Why: The New Science of Cause and Effect: by Judea Pearl and Dana Mackenzie, Basic Books (2018). ISBN: 978-0465097609.

[4] Tu, R., Zhang, K., Kjellström, H., & Zhang, C. (2022). Optimal transport for causal discovery. In *ICLR 2022-The Tenth International Conference on Learning Representations (Virtual), Apr 25th-29th, 2022.

[5] Kalisch, Markus, and Peter Bühlman. “Estimating high-dimensional directed acyclic graphs with the PC-algorithm.” Journal of Machine Learning Research 8.3 (2007).

[6] Xun Zheng, Bryon Aragam, Pradeep Ravikumar, and Eric P. Xing. 2018. DAGs with NO TEARS: continuous optimization for structure learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18). Curran Associates Inc., Red Hook, NY, USA, 9492–9503.

[7] D. M. Chickering and D. Heckerman. Efficient approximations for the marginal likelihood of Bayesian networks with hidden variables. Machine Learning, 29(2-3):181–212, 1997.

[8] D. Heckerman, D. Geiger, and D. M. Chickering. Learning Bayesian networks: The combination of knowledge and statistical data. Machine learning, 20(3):197–243, 1995.

[9] J. Kuipers, G. Moffa, and D. Heckerman. Addendum on the scoring of gaussian directed acyclic graphical models. The Annals of Statistics, pages 1689–1691, 2014.

[10] F. Fu and Q. Zhou. Learning sparse causal Gaussian networks with experimental intervention: Regularization and coordinate descent. Journal of the American Statistical Association, 108(501):288–300, 2013.

[11] Zheng, X., Aragam, B., Ravikumar, P. K., & Xing, E. P. (2018). Dags with no tears: Continuous optimization for structure learning. Advances in Neural Information Processing Systems, 31.

[12] Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A., & Jordan, M. (2006). A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(10).

[13] Matthew J. Vowels, Necati Cihan Camgoz, and Richard Bowden. 2022. D’ya Like DAGs? A Survey on Structure Learning and Causal Discovery. ACM Comput. Surv. Just Accepted (March 2022). https://doi.org/10.1145/3527154

[14] Starmans, R. (2020). Prometheus unbound or Paradise regained: the concept of Causality in the contemporary AI-Data Science debate. Journal de la Société Française de Statistique, 161(1), 4-41.

[15] Cheeseman, P. (1985). In defense of probability. In Proceedings of the Ninth International Joint Conference on AI (IJCAI, 1983).

[16] Williamson, J. (2009). Probabilistic theories of causality. The Oxford handbook of causation, 185-212.

[17] Good, I. J. (1959). A theory of causality. The British Journal for the Philosophy of Science, 9(36), 307-310.

[18] Good, I. J. (1961). A causal calculus (I). The British journal for the philosophy of science, 11(44), 305-318.

[19] Good, I. J. (1961). A causal calculus (II). The British journal for the philosophy of science, 12(45), 43-51.

[20] Pearl, J. (2009). Causal inference in statistics: An overview. Statistics surveys, 3, 96-146.

2020-2022最新论文列表

1. Jalaldoust, A., Hlaváčková-Schindler, K., & Plant, C. (2022, June). Causal Discovery in Hawkes Processes by Minimum Description Length. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 6, pp. 6978-6987).【高维Hawkes序列中的Grange causal graph learning】
2. Zhang, H., Zhang, K., Zhou, S., Guan, J., & Zhang, J. (2021, May). Testing independence between linear combinations for causal discovery. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 35, No. 7, pp. 6538-6546).【线性非高斯结构方程模型下两个线性组合之间的独立性——条件独立性测试中的一个特殊问题】
3. Lu, N. Y., Zhang, K., & Yuan, C. (2021, May). Improving causal discovery by optimal bayesian network learning. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 35, No. 10, pp. 8741-8748).【提出了一种基于分数的方法中, 一种新的穷举优化方法】
4. Hyttinen, A., Eberhardt, F., & Järvisalo, M. (2014, July). Constraint-based Causal Discovery: Conflict Resolution with Answer Set Programming. In UAI (pp. 340-349).【将因果图搜索问题, 视为带约束的优化问题】
5. Dhir, A., & Lee, C. M. (2020, April). Integrating overlapping datasets using bivariate causal discovery. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 34, No. 04, pp. 3781-3790).【从多个数据集中学习一致的因果结构的问题】
6. Huang, B., Zhang, K., Gong, M., & Glymour, C. (2020, April). Causal discovery from multiple data sets with non-identical variable sets. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 34, No. 06, pp. 10153-10161).【具有不同变量集的多个数据集的因果发现】
7. Maeda, T. N., & Shimizu, S. (2020, June). RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In International Conference on Artificial Intelligence and Statistics (pp. 735-745). PMLR.【受潜在混杂因素影响的数据中, 发现利用函数模型来发现因果(以往通常是基于约束)】
8. Tu, R., Zhang, C., Ackermann, P., Mohan, K., Kjellström, H., & Zhang, K. (2019, April). Causal discovery in the presence of missing data. In The 22nd International Conference on Artificial Intelligence and Statistics (pp. 1762-1770). PMLR.【缺失数据中的因果发现】
9. Feng, G., Yu, K., Wang, Y., Yuan, Y., & Djurić, P. M. (2020, May). Improving convergent cross mapping for causal discovery with Gaussian processes. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 3692-3696). IEEE.【耦合时间序列之间的因果发现】
10. Lippe, P., Cohen, T., & Gavves, E. (2021). Efficient neural causal discovery without acyclicity constraints. arXiv preprint arXiv:2107.10483.【一个基于神经网络+score based的因果发现】
11. Tu, R., Zhang, K., Kjellström, H., & Zhang, C. (2022). Optimal transport for causal discovery. In ICLR 2022-The Tenth International Conference on Learning Representations (Virtual), Apr 25th-29th, 2022.【用最优传输理论重写了FCM的方法, 并以优化的形式做优化, 实现因果发现】
12. Zhu, S., Ng, I., & Chen, Z. (2019, September). Causal Discovery with Reinforcement Learning. In International Conference on Learning Representations.【这个文章里对各类优化方法有比较好的调研】
13. Huang, B., Zhang, K., Gong, M., & Glymour, C. (2019, May). Causal discovery and forecasting in nonstationary environments with state-space models. In International conference on machine learning (pp. 2901-2910). PMLR.【非平稳时间序列中的因果发现】
14. Empirical Bayesian Approaches for Robust Constraint-based Causal Discovery under Insufficient Data【小数据、非平稳】
15. Brouillard, P., Lachapelle, S., Lacoste, A., Lacoste-Julien, S., & Drouin, A. (2020). Differentiable causal discovery from interventional data. Advances in Neural Information Processing Systems, 33, 21865-21877.【弱忠诚假设的因果发现】
16. Mokhtarian, E., Akbari, S., Ghassami, A., & Kiyavash, N. (2021, August). A recursive markov boundary-based approach to causal structure learning. In The KDD’21 Workshop on Causal Discovery (pp. 26-54). PMLR.【基于约束的方法, 用递归的优化方法】

值得关注的最新工作

1. Bhattacharya, R., Nagarajan, T., Malinsky, D., & Shpitser, I. (2021, March). Differentiable causal discovery under unmeasured confounding. In International Conference on Artificial Intelligence and Statistics (pp. 2314-2322). PMLR.【confounded systems中的因果图模型发现, 其中节点的定义可能不一样】
2. Brouillard, P., Lachapelle, S., Lacoste, A., Lacoste-Julien, S., & Drouin, A. (2020). Differentiable causal discovery from interventional data. Advances in Neural Information Processing Systems, 33, 21865-21877.【和上面的有点像】
3. S. Ren, H. Yin, M. Sun and P. Li, “Causal Discovery with Flow-based Conditional Density Estimation,” 2021 IEEE International Conference on Data Mining (ICDM), 2021, pp. 1300-1305, doi: 10.1109/ICDM51629.2021.00161.【流模型来估计变量的联合概率密度, 根据条件密度估计的方差推断每个潜在因果方向的分数, 我们的因果发现方法减轻了传统方法所做的限制性假设, 更好地捕捉各种问题领域中以任意形式出现的数据之间的复杂因果关系】
4. Zhang, H., Zhou, S., Zhang, K., & Guan, J. (2022, June). Residual Similarity Based Conditional Independence Test and Its Application in Causal Discovery. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 5, pp. 5942-5949).【CI转优化问题】

---

ToolBox

• gCastle URL

gCastle是华为诺亚方舟实验室自研的因果结构学习工具链, 主要的功能和愿景包括:

1. 数据生成及处理: 包含各种模拟数据生成算子, 数据读取算子, 数据处理算子(如先验灌入, 变量选择, CRAM)。
2. 因果图构建: 提供了一个因果结构学习python算法库, 包含了主流的因果学习算法以及最近兴起的基于梯度的因果结构学习算法。
3. 因果评价: 提供了常用的因果结构学习性能评价指标, 包括F1, SHD, FDR, TPR, FDR, NNZ等

• Causal Discovery Toolbox URL

The Causal Discovery Toolbox is a package for causal inference in graphs and in the pairwise settings for Python>=3.5.
Tools for graph structure recovery and dependencies are included. The package is based on Numpy, Scikit-learn, Pytorch and R.

• Tigramite URL

Tigramite 是一个因果时间序列分析 python 包。它允许从高维时间序列数据集有效地重建因果图, 并对获得的因果依赖进行建模,
以进行因果中介和预测分析。因果发现基于适用于离散或连续值时间序列的线性和非参数条件独立性测试。

• 包含的因果发现方法: PCMCI、PCMCIplus、LPCMCI
• 包含的独立性测试方法: ParCorr、GPDC / GPDCtorch、CMIknn、CMIsymb

• causalDisco: an R package with tools for causal discovery on observational data URL

causalDisco 包括temporal PC的实现

• Causal Discovery Tools for Time Series Applications - A Collection of Tutorials URL

为大气科学家数据分析工具 (DATAS) 网关的一部分, 编写的教程侧重于大气科学应用。数据: https://datasgateway.colostate.edu/

本资料库中解释的方法侧重于观察性研究, 其中不进行受控实验(例如, 气候中的有针对性的建模研究)来确定原因和影响。
这些方法允许您识别需要使用我们现有的特定应用领域知识进一步验证的”潜在”关系。

方法包括: 二元格兰杰因果检验、PC稳定算法的时间序列扩展

Related work with code

[1] TCDF: Causal Discovery with Attention-Based Convolutional Neural Networks URL

时间因果发现框架 (TCDF) 是在 PyTorch 中实现的深度学习框架。给定多个时间序列作为输入, TCDF 发现这些时间序列之间的因果关系并输出因果图。
它还可以根据其他时间序列预测一个时间序列。TCDF 使用基于注意力的卷积神经网络结合因果验证步骤。通过解释卷积网络的内部参数, TCDF 还可以发现因果之间的时间延迟。

[2] Amortize Causal Discovery: Learning to Infer Causal Graphs from Time-Series Data URL

通过 Amortized Causal Discovery, 我们学习从具有不同潜在因果图但共享动态的样本中推断因果关系。这使我们能够跨样本进行泛化, 从而通过增加训练数据大小来提高我们的性能。

[3] Causal Discovery from Nonstationary/Heterogeneous Data: Skeleton Estimation and Orientation Determination. IJCAI 2017. URL

[4] Causal Discovery in Heavy-Tailed Models URL

[5] Differentiable Causal Discovery from Interventional Data URL

[6] Generalized Score Functions for Causal Discovery. KDD, 2018 URL

具有广义得分函数的贪婪等价搜索的因果结构学习(适用于混合连续和离散数据、具有高斯或非高斯分布的数据、线性或非线性因果机制以及具有多维的变量。)

[7] Learning the Causal Structure of Copula Models with Latent Variables. UAI. 2018 URL

[8] Data Generating Process to Evaluate Causal Discovery Techniques for Time Series Data, at the Causal Discovery & Causality-Inspired Machine Learning Workshop at NeurIPS 2020. URL

[9] Process Mining Meets Causal Machine Learning: Discovering Causal Rules from Event Logs URL